
Trabajar con programas de hojas de cálculo como Excel ofrece una infinidad de posibilidades gracias al uso de diferentes fórmulas y ecuaciones. Las funciones disponibles cubren casi cualquier necesidad que tengamos para nuestros documentos académicos como profesionales. Hoy nos centraremos en concreto en la cuestión de cómo calcular la desviación típica en Excel.
¿Qué es la desviación típica?
Este concepto es muy importante a la hora de realizar cálculos estadísticos. Es conocido también con los nombres de desviación estándar o desvío típico, siendo representada de manera abreviada con la minúscula de la letra griega minúscula sigma (σ) o bien la letra latina «s». También suele representarse con las siglas SD, del inglés standard deviation.
Este medidor se utiliza para cuantificar la variación o la dispersión de un conjunto o muestra de datos numéricos. La desviación estándar es siempre mayor o igual a cero. Cuando el grado de desviación es bajo (cercano al cero), significa que la mayor parte de los datos se concentran cerca de la media; en cambio un grado de desviación alto indica que los datos están más dispersos y cubren un rango de valores más amplio.
El cálculo de la desviación típica puede tener aplicaciones muy prácticas en determinados estudios estadísticos. Su mayor utilidad es permitirnos conocer el grado de dispersión media de una variable, es decir, cuanto se alejan los diferentes valores de un grupo respecto al valor promedio.
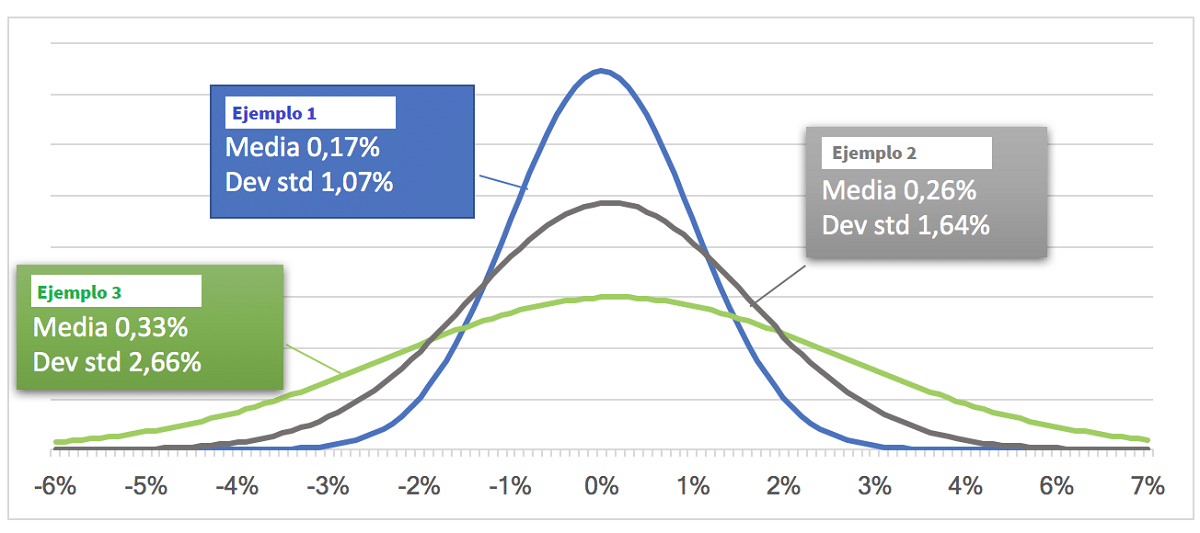
Tres ejemplos distintos de la relación entre la media y la desviación típica
El gráfico que hay sobe estas líneas ilustra tres ejemplos diferentes de desviación típica: alta, media y baja, cada una de ellas relacionado con un determinado valor medio.
Un modo muy burdo de explicarlo es con el siguiente ejemplo. Dos casos diferentes:
- Caso 1: Imaginemos un grupo de hermanos de 38, 40 y 42 años. La media es de 40, pero la desviación típica es menor, pues todos los valores se encuentran cerca de ella, con valores que solamente están a dos años de diferencia con el valor medio.
- Caso 2: Ahora imaginemos que las edades de los hermanos son 25, 40 y 55 años. La media seguirá siendo 40, pero la dispersión es mayor. Es decir, la desviación típica es mayor, con valores que distan quince años del valor medio.
Conociendo la media y la desviación estándar de la distribución de una serie de datos, es posible calcular la probabilidad de obtener un resultado superior o inferior respecto a un determinado valor. Aunque para muchos puede parecer abstracto, este cálculo tiene implicaciones muy significativas en la formulación de modelos financieros, por ejemplo.
Pero en lugar de correr el riesgo de perdernos en laberintos matemáticos, centrémonos en la pregunta principal y tema central de nuestro post: cómo calcular la desviación típica en Excel.
Cómo calcular la desviación típica en Excel
Ejecutar este cálculo matemático en una hoja de trabajo de Excel es bastante sencillo y muy rápido. Para conseguirlo tendremos que seguir estos pasos:
- En primer lugar obviamente habrá que entrar en Microsoft Excel y acceder a la hoja de cálculo que contiene los datos a partir de los cuales queremos obtener la desviación típica.
- A continuación debemos introducir los valores que queremos utilizar. Para esto escogeremos una columna y escribiremos el valor de cada dato en cada una de las celdas.
- Una vez que hayamos ingresado todos los datos en la columna elegida, el siguiente paso consistirá en hacer clic en una celda en blanco. Esa es la celda elegida para el resultado en la cual aparecerá el valor de la desviación típica.
- Arriba en la barra introduciremos la fórmula de la desviación estándar para la celda vacía que hemos seleccionado. La fórmula es esta:
=DESVEST.P (XX:XX)
DESVEST es la abreviatura de «desviación estándar», mientras que la P significa población», es decir, «muestra». Los valores que van en los paréntesis corresponden a las celdas seleccionadas que contienen los diferentes valores de dicha muestra.
- El siguiente paso es asignar el rango de valores sobre el cual Excel va a realizar el cálculo. Este debe ser introducido correctamente entre los paréntesis. Allí hay que escribir la letra y el número de cada celda. Si las celdas son correlativas por ejemplo, desde A2 a A20, simplemente escribiremos la primera y la última separadas por dos puntos (:). Siguiendo este ejemplo, sería así: =DESVEST.P (A2:A20).
- El último paso es pulsar la tecla «Enter» para que Excel aplique la fórmula y muestre el resultado en la celda seleccionada al principio.
La función DESVESTA de Microsoft Excel usa la siguiente fórmula:
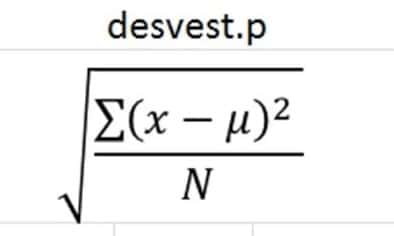
Donde la «x» toma el valor de la media de muestra promedio (valor1, valor2,…) y la «n» representa el tamaño de la misma.
Otros cálculos estadísticos con Excel
Además de saber cómo calcular la desviación típica en Excel, es muy probable que a la hora de organizar datos en nuestras hojas de trabajo tengamos que recurrir a otras fórmulas. Las más habituales son las que nos permiten calcular valores como la media, la mediana, la moda y la varianza.
Media
Como todo el mundo sabe, la media (también llamada media aritmética) es el resultado de sumar los diferentes valores numéricos y dividirlos entre el número total de elementos de una serie. Para obtener la media, el sistema es prácticamente el mismo que usamos para cómo calcular la desviación típica en Excel. La única diferencia es la fórmula que se aplica, que en este caso es esta: =PROMEDIO(valorX:valorY).
Mediana
La mediana de un conjunto de números, que muchas veces se confunde con la media, es aquel valor que se encuentra en la posición media de una serie. No tiene por qué coincidir con la media. La fórmula que se aplica para su cálculo en Excel es: =MEDIANA(valorX:valorY).
Moda
La moda de un conjunto de números es aquel valor que se repite más veces. Tampoco tiene que coincidir necesariamente ni con la media ni con la mediana. La fórmula para calcularlo en Excel es esta: =MODA(valorX:valorY).
Varianza
Este concepto es algo más complejo que los anteriores. La varianza está estrechamente ligado a la media y a la desviación típica. Es otro modo de medir la dispersión de un conjunto de valores numéricos, solo que referido a la «distancia» en la que un conjunto de valores se aleja con respecto a la media. La fórmula: =VAR(valorX:valorY).